In 1978, Malthus developed a model for human growth population that is also commonly used to model bacterial growth as follows. Let N(t) be the population density observed at time t. Let K be the rate of reproduction per unit time. Neglecting population deaths, the population density at a time t + Δt (with small Δt) is given by

N(t + Δt) ≈ N(t) + KN(t)Δt

which also can be written as

Since N(t) can be considered to be a very large number, letting Δt → 0 gives the following differential equation (Edelstein-Keshet, 2005):

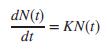
a. Assuming an initial population N(0) = N₀, solve the differential equation by finding N(t).

b. Find the time at which the population is double the initial population.

Transcribed Image Text:

N(t + At) – N(t) KN(t) At