Prior to the discovery of any specific public-key schemes, such as RSA, an existence proof was developed
Question:
Prior to the discovery of any specific public-key schemes, such as RSA, an existence proof was developed whose purpose was to demonstrate that public-key encryption is possible in theory. Consider the functions \(\mathrm{f}_{1}\left(x_{1}ight)=z_{1} ; \mathrm{f}_{2}\left(x_{2}, y_{2}ight)=z_{2} ; \mathrm{f}_{3}\left(x_{3}, y_{3}ight)=z_{3}\), where all values are integers with \(1 \leq x_{i}, y_{i}, z_{i} \leq N\). Function \(\mathrm{f}_{1}\) can be represented by a vector M1 of length \(N\), in which the \(k\) th entry is the value of \(\mathrm{f}_{1}(k)\). Similarly, \(\mathrm{f}_{2}\) and \(\mathrm{f}_{3}\) can be represented by \(N \times N\) matrices M2 and M3. The intent is to represent the encryption/decryption process by table lookups for tables with very large values of \(N\). Such tables would be impractically huge but could be constructed in principle. The scheme works as follows: Construct M1 with a random permutation of all integers between 1 and \(N\); that is, each integer appears exactly once in M1. Construct M2 so that each row contains a random permutation of the first \(N\) integers. Finally, fill in M3 to satisfy the following condition:
\[\mathrm{f}_{3}\left(\mathrm{f}_{2}\left(\mathrm{f}_{1}(k), pight), kight)=p \quad \text { for all } k, p \text { with } 1 \leq k, p \leq N\]
To summarize,
1. M1 takes an input \(k\) and produces an output \(x\).
2. M2 takes inputs \(x\) and \(p\) giving output \(z\).
3. M3 takes inputs \(z\) and \(k\) and produces \(p\).
The three tables, once constructed, are made public.
a. It should be clear that it is possible to construct M3 to satisfy the preceding condition. As an example, fill in M3 for the following simple case:
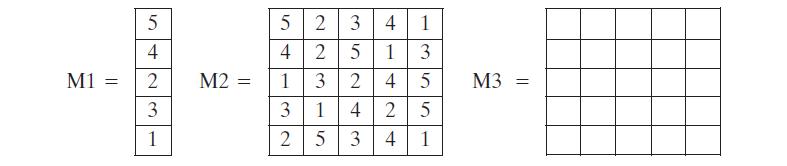
Convention: The \(i\) th element of M1 corresponds to \(k=i\). The \(i\) th row of M2 corresponds to \(x=i\); the \(j\) th column of M2 corresponds to \(p=j\). The \(i\) th row of M3 corresponds to \(z=i\); the \(j\) th column of M3 corresponds to \(k=j\).
b. Describe the use of this set of tables to perform encryption and decryption between two users.
c. Argue that this is a secure scheme.
Step by Step Answer:
This proof is discussed in the CESG report mentioned in Chapter 9 ...View the full answer
