Show that, with n relations, there are (2(n−1))!∕(n−1)! different join orders. A complete binary tree is one where every internal node has exactly two children. Use the fact that the number of different complete binary trees with n leaf nodes is: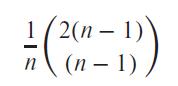

If you wish, you can derive the formula for the number of complete binary trees with n nodes from the formula for the number of binary trees with n nodes. The number of binary trees with n nodes is: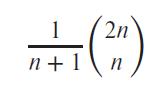

This number is known as the Catalan number, and its derivation can be found in any standard textbook on data structures or algorithms.

1/2(n-1)) (n-1) B) n