Most errors in billing insurance providers for health care services involve honest mistakes by patients, physicians, or others involved in the health care system. However, fraud is a serious problem. The National Health Care Anti-Fraud Association estimates that approximately \(\$ 68\) billion is lost to health care fraud each year. Often when fraud is suspected, an audit of randomly selected billings is conducted. The selected claims are reviewed by experts and each claim is classified as allowed or not allowed. The claims not allowed are considered to be potentially fraudulent. In general, the distribution of claims is highly skewed such that the majority of claims filed are small claims and only a few are large claims. Since simple random sampling would likely be overwhelmed by small claims, claims chosen for auditing are sampled in a stratified way: a set number of claims are sampled from each category of claim size: small, medium, and large. Here are data from an audit that used stratified sampling from three strata based on the claim size (i.e., monetary amount of the claim).

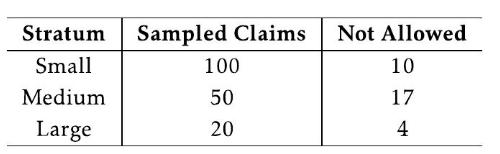
(a) Can these data be used to estimate the proportion of large claims for which fraud might be expected?

(b) Can these data be used to estimate the proportion of possibly fraudulent claims that are large claims?

(c) Construct a \(2 \times 3\) contingency table of counts for these data and include the marginal totals, with the rows being the classification of claims and the columns being the size of the claim.

(d) Calculate the expected number of claims that would not be allowed among the large claims, under the hypothesis of no association of between size of claim and the claim not being allowed.

(e) Is the use of the chi-square statistic justified for these data?

(f) A chi-square test of no association between size of claim and whether it was allowed has value 12.93. How many degrees of freedom does the chi-square statistic have and what is the \(p\)-value for a test of no association?
(g) Compute the \(\chi^{2}\) residuals. Based on the residuals, interpret the findings in the context of the data.

Transcribed Image Text:

Stratum Small Sampled Claims Not Allowed 100 10 Medium 50 17 Large 20 4