Solve the problem P3.7 using the Laplace transformation technique.

Problem P3.7

Consider the cantilever of the atomic force microscope (Binning and Quate, 1986) with length \(=100 \mu \mathrm{m}\), thickness \(=0.8 \mu \mathrm{m}\), and width \(=20 \mu \mathrm{m}\). The material of the cantilever is silicon nitride having \(E=310 \times 10^{9} \mathrm{~Pa}\) and density \(=3.29 \mathrm{gm} / \mathrm{cc}\). A force \(f(t)\) is applied at the tip of the cantilever.

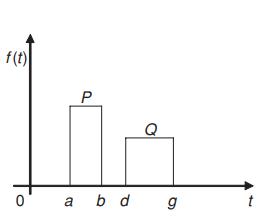
The force \(f(t)\) is as shown in Figure P3.7 for which \(P=1 \mu \mathrm{N}, Q=\) \(0.5 \mu \mathrm{N}, a=1 \mathrm{sec}, b=2 \mathrm{sec}, d=3 \mathrm{sec}\), and \(g=5 \mathrm{sec}\).

a. On the basis of an equivalent SDOF model, find the unit impulse response function for zero initial conditions. Assume the damping ratio \(=0.001\).

b. Using the convolution integral, determine \(x(t)\) for \(t>0\). Assume that \(x(0)=0.5 \mu \mathrm{m}\), and \(d x / d t=0\).

Using MATLAB, plot \(x(t)\) versus \(t\).

Figure P3.7

f(t) P 0 abd g t