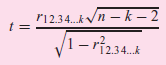Assuming that Y and X₂, X₃, . . . , X_kare jointly normally distributed and assuming that the null hypothesis is that the population partial correlations are individually equal to zero, R. A. Fisher has shown that

follows the t distribution with n ˆ’ k ˆ’ 2 df, where k is the kth-order partial correlation coefficient and where n is the total number of observations. (r_{1 2.3} is a firstorder partial correlation coefficient, r_{1 2.3 4} is a second-order partial correlation coefficient, and so on.) Refer to Exercise 7.2. Assuming Y and X₂ and X₃ to be jointly normally distributed, compute the three partial correlations r_{1 2.3}, r_{1 3.2}, and r_{2 3.1} and test their significance under the hypothesis that the corresponding population correlations are individually equal to zero.

'n k 2 P12.34.k/n - k - 2 t = |1 r2,34.k