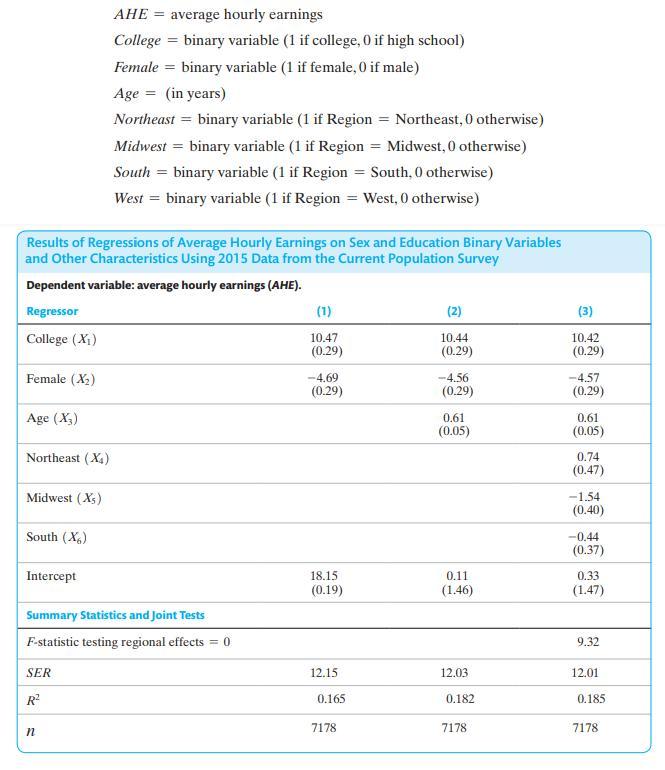
Question: Using the regression results in column (1): a. Is the college-high school earnings difference estimated from this regression statistically significant at the 5% level? Construct
Using the regression results in column (1):
a. Is the college-high school earnings difference estimated from this regression statistically significant at the 5\% level? Construct a \(95 \%\) confidence interval of the difference.
b. Is the male-female earnings difference estimated from this regression statistically significant at the \(5 \%\) level? Construct a \(95 \%\) confidence interval for the difference.
AHE average hourly earnings College = binary variable (1 if college, 0 if high school) Female = binary variable (1 if female,0 if male) Age = (in years) Northeast = binary variable (1 if Region = Northeast, 0 otherwise) Midwest = binary variable (1 if Region Midwest, 0 otherwise) South = binary variable (1 if Region = South, 0 otherwise) West = binary variable (1 if Region = West, 0 otherwise) Results of Regressions of Average Hourly Earnings on Sex and Education Binary Variables and Other Characteristics Using 2015 Data from the Current Population Survey Dependent variable: average hourly earnings (AHE). Regressor (1) College (X1) Female (X2) Age (X3) Northeast (X4) Midwest (X's) (2) (3) 10.47 10.44 10.42 (0.29) (0.29) (0.29) -4.69 -4.56 (0.29) (0.29) -4.57 (0.29) 0.61 (0.05) 0.61 (0.05) 0.74 (0.47) -1.54 (0.40) South (X) -0.44 (0.37) Intercept 18.15 0.11 (0.19) (1.46) 0.33 (1.47) Summary Statistics and Joint Tests F-statistic testing regional effects =0 9.32 SER 12.15 12.03 12.01 R 0.165 0.182 0.185 7178 7178 7178 n
Step by Step Solution
3.41 Rating (145 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


