Question: OPQ is a triangle. a. Show that OS(vector) = 2a + b. b. Point T is added to the diagram such that OT(vector) = b.

OPQ is a triangle.


2PR RQ and 3OR = OS OP = a and 00 =a. Show that OS(vector) = 2a + b.


b. Point T is added to the diagram such that OT(vector) = −b. Prove that points T, P and S lie on a straight line.


b. 18 =

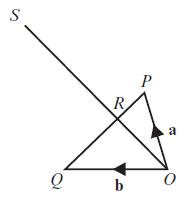
2PR RQ and 3OR = OS OP = a and 00 = b. 18 =

Step by Step Solution

★★★★★

3.49 Rating (162 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

To prove the given statements lets analyze the given information and apply vector operations and pro... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Edexcel AS And A Level Mathematics Questions!

Q:

P - F: 6 - 2 8 A Accounting for inventory using the perpetual inventory system - FIFO, LIFO, and weighted - average ( Learning Objectives 2 , 3 ) Fit Gym began January with merchandise inventory of 7...

Q:

The diagram shows two circles, C 1 and C 2 , touching at the point T. Circle C 1 has centre P and radius 8 cm; circle C 2 has centre Q and radius 2 cm. Points R and S lie on C 1 and C 2 respectively,...

Q:

The points R and S lie on a circle with centre C(a, 2), as shown in the diagram. The point R has coordinates (2, 3) and the point S has coordinates (10, 1). M is the midpoint of the line segment RS....

Q:

The reaction A2(g) + B(g) A(g) + AB(g) has an equilibrium constant of Kp = 2. The accompanying diagram shows a mixture containing A atoms (red), A2 molecules, and AB molecules (red and blue). How...

Q:

Give correct answers only 5. In the figure below, DE = 12 AB and BC = 2/3 BD and the co ordinates of A.B and D are (5,4),(9,6) and ( 12,0) respectively. B(9,6) A(5,4) D(12,0) Find the vectors (1) BD...

Q:

Please answer all 24 of these geometry practice questions, you can also add a small explanation along with the answer, but its up to you, not a requirement. 1. (165) Is the following sentence true?...

Q:

A Quiz: 07.08 Concept 7.1: Let's x * Course Hero A springfieldpublicschools.instructure.com/courses/1715684/quizzes/7578295/take G A 2023 School Year: Q4-Q4 LA... D Question 1 2 pts Home...

Q:

Kindly provide correct answers 10. In the figure OABC is a trapezium in which 3 AB = 20C. S divides OC in the ratio 2:1 and AS produced meets BC produced at T Given that OC = 3c and OA = a (a)...

Q:

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

Q:

Consider the trigonometric series a0 2 + X r=1 (ar cos rx + br sin rx) where a0, a1, a2, . . . and b1, b2, . . . are constants and suppose that f(x) is a periodic function of x with period 2. (a)...

Q:

Chapter Thirteen A FUNDAMENTAL TOOL: VECTORS Contents 13.1 Displacement Vectors . . . . . . . . . . . . 686 Notation and Terminology . . . . . . 686 Addition and Subtraction of Displacement Vectors ....

Q:

You are to create your own version of a string class named myString. myString will store a character string of up to 25 characters (how will you handle more than 25?). The string of characters must...

Q:

In Figure two semicircular arcs have radii R2 = 7.80 cm and R1 = 3.15 cm, carry current i = 0.281 A, and share the same center of curvature C. What are the (a) Magnitude and (b) Direction (into or...