Question: Consider the crack problem shown for the anti-plane strain case with u = v = 0, w = w(x,y). From Section 7.4, the governing equation

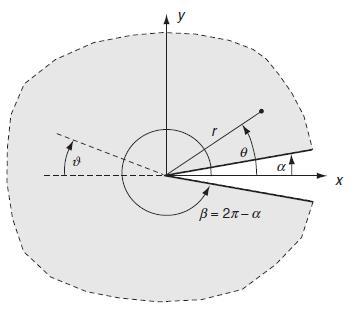
Consider the crack problem shown for the anti-plane strain case with u = v = 0, w = w(x,y). From Section 7.4, the governing equation for the unknown displacement component with zero body force was given by Laplace’s equation, which in polar coordinates reads.

7 aw 1 dw + r r dr 1 3 w ar 30 0

Use a separation of variables scheme with w = f (0), where is a parameter to be determined and f (0) is

Data from section 8.4.10

Consider the original wedge problem shown in Fig. 8.16 for the case where angle a is small and is 2 - . This

0 B = 2- X

while the identical conditions at 0=6=27- = 2 produce sin 2 (2 2) ^ 2 si - sin 272C +[cos 2(2-2) - cos 2] =

Near the tip of the notch 0 and the stresses will be of order O(2), while the displacements are O(-1). At

$Such relations play an important role in fracture mechanics by providing information on the nature of the$

The remaining constants A and B are determined from the far-field boundary conditions. However, an important

Data from section 7.4

or traction form: T = T(x,y) = tnx + t2ny (b) dw My 1.) the on dy = w nx +. x on S (7.4.7) The solution to

D 10w + = + 2 20 r r aw 1 dw dr2 0

Step by Step Solution

★★★★★

3.50 Rating (160 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Using w Ar f0 in Vw0 KKDr Wr hr 0 fK 0 f Solution f Asin 20 B cos 20 Cho... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Elasticity Theory Applications Questions!

Use mesh analysis to find the current io in the circuit in Fig. 3.95? Figure 3.95 4 2 10 8 310

For the mode III crack problem in Exercise 8.44, explore the strain energy in a circular area of radius R centered at the crack tip. Refer to the discussion in Section5.8 anduse relation (6.1.10) to...

Consider the case of a crack problem in an anisotropic monoclinic material under anti-plane deformation as described in Exercise 11.16. Following relation (11.6.6), choose the complex potential form...

For the anti-plane stain crack problem solved in Exercise 8.44, plot contours of the displacement and stress fields. Data from exercise 8.44 Consider the crack problem shown for the anti-plane strain...

This question involves the use of AGGREGATE linear PYTHOIN regression on the Auto data set. (a) Perform a simple linear regression with mpg as the response and horsepower as the predictor. Describe...

function = explicit(mx) %% Problem Number: 49 L = 45; tmax = 80; U = 0.8; D = 1.2; Xs = 4; Cs = 10; XFlux = 36; % % % % % % % m s m/s m2/s m kg/m m % Calculating dx and dt based of mx input dx =...

HW 12, MAT 312/AMS 351: SPRING 2017 Problem 1. (1) Set H = {4a + 6b | a, b Z} Z. Show that H is a subgroup of Z. (2) Is H cyclic? Problem 2. Write down all the cyclic subgroups of the following...

Consider an anisotropic monoclinic material symmetric about the x,y-plane (see Fig. 11.2) and subject to an anti-plane deformation specified by u = v = 0, w = w(x,y). Show that in the absence of body...

A. B. A. B. ( ( ) ) Beginning and Intermediate Algebra An open source (CC-BY) textbook Available for free download at: http://wallace.ccfaculty.org/book/book.html by Tyler Wallace 1 ISBN...

Instuctor's Annotated Edition TENTH EDITION Understandable Statistics Concepts and Methods Charles Henry Brase Regis University Corrinne Pellillo Brase Arapahoe Community College Australia Brazil...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

Without energy companies, the world would lack health care, farm equipment, automobiles, indoor plumbing, and computers. Despite the many ways in which energy businesses improve the quality of life...

A parallel RLC circuit, which is driven by a variable-frequency 10-A source, has the following parameters: R=500ohm, L=0.5 mH, and C=20F. Find the resonant frequency, the BW, and the average...

S5-14 Compute cost per liter (Learning Objective 1) Refer to the Crystal Springs Filtration Department Data Set. 1. Compute the May conversion costs in the Filtration Department. 2. If the Filtration...

Let us say that your local Kirana store plans to open its local website. Develop the set of key pre-planning activities for web development.? P/85

Plot the solution of the equation 6y + y = f(t) if f (t) = 0 for t + 0 and f(t) = 15 for t 0. The initial condition is y(0) = 7.

Construct a Simulink model of the following problem. The forcing function is where g(t) = 10 sin 4t. 5x + sin x = = f(t) x(0) = 0

Use MATLAB to solve the following problem: x - 3y = 2 x + 5y = 18 4x - 6y = 10

Lathe bed is made of___.I am not satisfy give downvote (A) cast iron (B) cast steel (C) mild steel (D) pig iron

assuming all other requirements are met which of the following taxpayers qualify for the 2022 earned income credit

What is the generation-skipping transfer tax, and who is the skip person?