For the hollow elliptical section in Example 9.5, explicitly show that the given stress function (9.6.1) will yield the constant value specified by (9.6.2) on the inner boundary. Next using the methods from Example 9.1, show that the general torque relation (9.3.31) will also produce the result (9.6.3). Finally verify the maximum shear stress relation (9.6.4).

Data from example 9.5

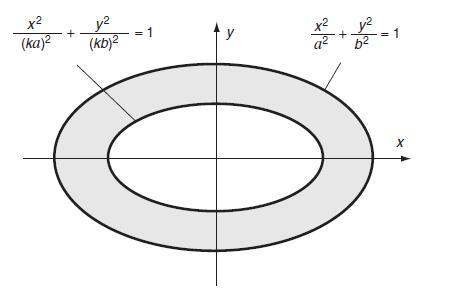
Equation 9.6.1

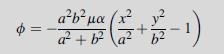
Equation 9.6.2

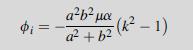
Equation 9.3.31

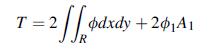
Equation 9.6.3

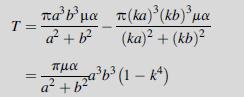
Equation 9.6.4

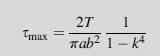
Consider the torsion of a bar with a hollow elliptical section as shown in Fig. 9.15. The inner boundary is simply a scaled ellipse similar to that of the outer boundary. Using the solid section solution from Example 9.1, it can be shown that the contour lines, or lines of constant shear stress, coincide with such a scaled concentric ellipse (see Exercise 9.10). The shear stress will then be tangent to the inner boundary contour and no stress will then act on the lateral surface of a cylinder with inner ellipse section. Therefore, the solution to the hollow section can be found by simply removing the inner core from the solid solution developed in Example 9. 1, and this results in the same stress distribution in the remaining material. Thus, the stress function solution for the hollow case is given by (-) ab a a + b (9.6.1)