From Section 10.4, the complex potentials:

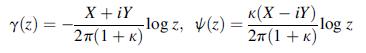
would be the appropriate forms for a problem in which the body contains a hole surrounding the origin (i.e., multiply connected). Show for this case that the complex displacement U is unbounded as IzI→0 and IzI→∞. Also, explicitly verify that the resultant force across any contour surrounding the origin is X + iY. Finally, determine the stress distribution on the circle r = a.

Data from section 10.4

Y(Z) = X +iY 2(1+K) -log z, y(z) = K(X iY) -log z 2(1 +K)