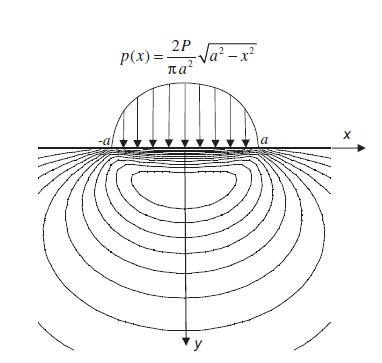
The example MATLAB code C.7 numerically integrated the integrals in solution (8.5.9) for the case of the flat rigid punch problem. Modify this example code to handle the case of the cylindrical punch given by solution (8.5.13) and thus generate the τ, _max contours shown in Fig. 8.43.

Equation 8.5.9

Equation 8.5.13

Fig 8.43

2y p(s) (xs) - [ - a [(x x) + y] -a 0x = = Txy = ds a = p(s) (x - s) ds 22 [(x x) + y] T -a 2Py - + 1. -a 2y ra p(s) 2Py ds = = = 2 L [(x 5) + y] -1. -a (x-s) - /a. - 3 [(x s ) + y] 4 a 22 - - ds 1 ds - [( x s) + 1 ] (x - s) a 3 [ ( x s) + y ] ds