Using the basic field equations for spherical coordinates given in Appendix A, formulate the elasticity problem for the spherically symmetric case, where u_R = u(R), u_∅ = u_θ = 0. In particular, show that the governing equilibrium equation with zero body forces becomes:

Data from appendix a

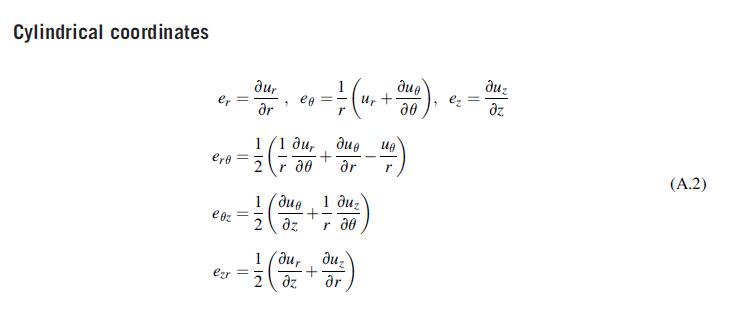
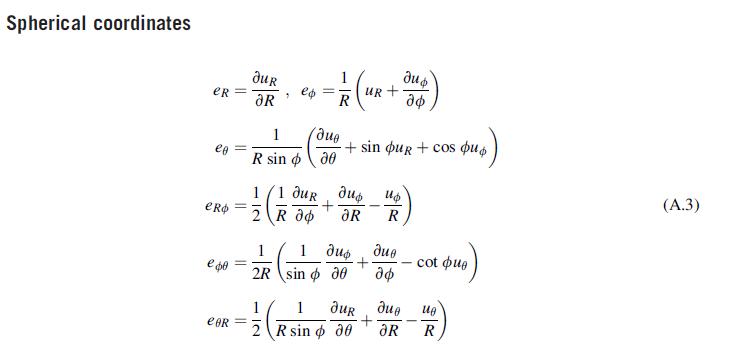
2 du 2 du + dR R dR R2 Next solve this equation and show that the general solution can be expressed as C u=CR+ OR = K - R2' 0=08=K+ where C, C2, K, and K are arbitrary constants. 2K2 R3, u=0 K2 R