Let X be a continuous random variable with p.d.f. fX, c.d.f. FX and finite nth raw moment, n ≥ 1.

(a) Assume that X is positive, i.e. Pr(X > 0) = 1. Prove that

by expressing 1 − FX as an integral, and reversing the integrals.

(b) Generalize (7.69) to

(c) Relaxing the positivity constraint, generalize (7.69) to

Even more generally, it can be shown that

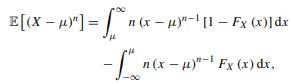
which the reader can also verify.

E[X] = [1 - Fx (x)] dr