Prove the following relations.

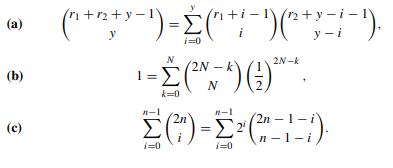
(a) Evaluate

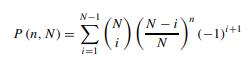
for n = 0 and n = 1. Verify by induction on n that P (n, N) = 1, 1 ≤ n ≤ N − 1, (1.60)
but that it does not hold for n ≥ N. How does P (N,N) behave as N grows? A probabilistic explanation of this interesting identity is given in Example 2.13 (with r = N) and Section 4.2.6.

(b) Prove that

Is Q (N,N) close to 0?

(c) Let

Prove by induction that M(N ) = N!. As an aside, it appears that, for any r ∈ R,

If you numerically confirm this, watch out for round-off error for large |r|.

(a) (b) (c) (1+1+y-1) y N i=0 2N-k i (1+y-i- y-i 2N-k 1 = (^~^) () ***. N (2n-1-i k=0 2n n-1-i i=0