Determine the finite population correction factor for each value of N and n.

(a) N = 1000 and n = 500 

(b) N = 1000 and n = 100

(c) N = 1000 and n = 75 

(d) N = 1000 and n = 50

(e) N = 100 and n = 50 

(f) N = 400 and n = 50

(g) N = 700 and n = 50 

(h) N = 1200 and n = 50

What happens to the finite population correction factor as the sample size n decreases but the population size N remains the same? as the population size N increases but the sample size n remains the same?

Use the information below.

In this section, you studied the construction of a confidence interval to estimate a population mean. In each case, the underlying assumption was that the sample size n was small in comparison to the population size N. When n ≥ 0.05N, however, the formula that determines the standard error of the mean σ_x needs to be adjusted, as shown below.

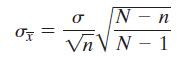
Recall from the Section 5.4 exercises that the expression √(N - n)/(N - 1) is called a finite population correction factor. The margin of error is

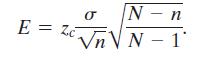
N-n Vn V N 1