Let \(X\) be a uniformly distributed random variable, and let us assume that we do not know where the support of this distribution is located, but we know that its width is 1 . Then, , where is the unknown expected value of \(X\), as well as the midpoint of the support. To estimate we take a sample of \(n=2\) independent realizations \(X_{1}\) and \(X_{2}\) of the random variable. Now consider the order statistics

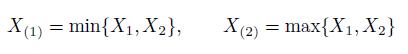
and the confidence interval

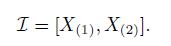
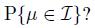What is the confidence level of  i.e., the probability  Both observations have a probability 05 of falling to the left or to the right of  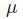. The confidence interval will not contain  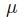if both observations fall on the same half of the support. Then, since \(X_{1}\) and \(X_{2}\) are independent, we have

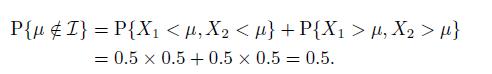
So, the confidence level for \(\mathcal{I}\) is the complement of this probability, i.e., \(50 \%\).

Now suppose that we observe \(X_{1}=0\) and \(X_{2}=06\). What is the probability that is included in the confidence interval \(\mathcal{I}\) resulting from Eq. (10.24), i.e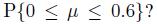 In general, this question does not make any sense, since is a number. But in this specific case, we have some additional knowledge, leading to the conclusion that the expected value is included in that interval for sure. Since the absolute deviation  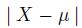from the expected value is bounded by 0.5 , a confidence interval of width 06 must contain  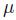. By a similar token, if we observe \(X_{1}=0\) and \(X_{2}=0.001\), we have some reason to argue that such a small interval is quite unlikely to include, but there is no way in which we can express this view properly, within the framework of orthodox statistics.

Data From Equation (10.24)

X~U[-0.5, +0.5]