(a) Solve the DE in Problem 28 subject to y(1) = 0. For convenience let k = v_r/v_s.

(b) Determine the values of v_s for which the swimmer will reach the point (0, 0) by examining lim _{x †’0+} y(x) in the cases k = 1, k > 1, and 0 < k > 1.

Data from problem 28

In the following figure (a) suppose that the y-axis and the dashed vertical line x = 1 represent, respectively, the straight west and east beaches of a river that is 1 mile wide. The river €“flows northward with a velocity v_r, where |v_r| = v_r mi/h is a constant. A man enters the current at the point (1, 0) on the east shore and swims in a direction and rate relative to the river given by the vector v_s, where the speed |v_s| = v_s mi/h is a constant. The man wants to reach the west beach exactly at (0,0) and so swims in such a manner that keeps his velocity vector v_s always directed toward the point (0, 0). Use figure (b) as an aid in showing that a mathematical model for the path of the swimmer in the river is

dy/dx = v_sy €“ v_rˆš(x² + y²)/v_sx.

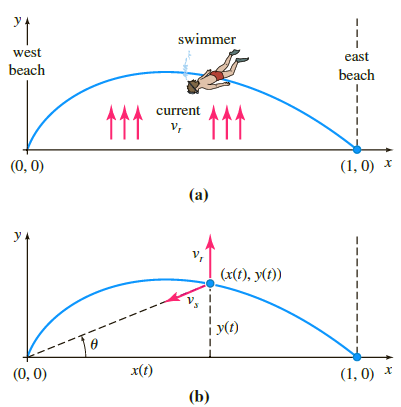
swimmer west east beach beach current v, (0, 0) (1, 0) x (a) y (x(t), y(t)) ) x(t) (0, 0) (1, 0) * (b)