Question: After a mass m is attached to a spring, it stretches it s units and then hangs at rest in the equilibrium position as shown

After a mass m is attached to a spring, it stretches it s units and then hangs at rest in the equilibrium position as shown in the following figure (b). After the spring/mass system has been set in motion, let x(t) denote the directed distance of the mass beyond the equilibrium position. As indicated in following figure (c), assume that the downward direction is positive, that the motion takes place in a vertical straight line through the center of gravity of the mass, and that the only forces acting on the system are the weight of the mass and the restoring force of the stretched spring. Use Hooke€™s law: The restoring force of a spring is proportional to its total elongation. Determine a differential equation for the displacement x(t) at time t > 0.

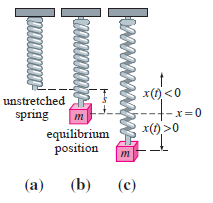
x()<0 unstretched spring x= 0 x() >0 equilibrium position (b) (a) (c) wwwwwwa

x() 0 equilibrium position (b) (a) (c) wwwwwwa

Step by Step Solution

★★★★★

3.28 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

We know that at equilibrium springs restorative force cancels that of gravity so tha... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (2 attachments)

1596_6062c74d00e50_675063.pdf

180 KBs PDF File

1596_6062c74d00e50_675063.docx

120 KBs Word File

Students Have Also Explored These Related First Course Differential Equations Questions!

In Problem 19, what is a differential equation for the displacement x(t) if the motion takes place in a medium that imparts a damping force on the spring/ mass system that is proportional to the...

A mass is attached to a spring, as in Example 6.92. At time t = 0 second, the spring is stretched to a length of 10 cm below its position at rest. The spring is released, and its length 10 seconds...

A mass m = 25 is attached to a unit spring with k = 1, and frictional coefficient = .01. The spring will break when it moves more than 1 unit. Ignoring the effect of the transient, what is the...

This print out should have 19 questions. be within + 3.0% Multiple choice questions may continue on the next column or page - find all choices 007 (part 1 of 3) 10.0 points before answering- A block...

In Exercises 1 - 16, plot the point given in polar coordinates and then give three different expressions for the point such that (a) r 0 and 0 (c) r > 0 and 2 9. (20, 3) In...

Hi! I have a quick multiple-choice homework that I'd appreciate any help on. thank you! Part 2: Open-Ended Responses. All work and correct units MUST be shown for full credit. BOX in final answer....

7. A satellite of mass 120 kg is in circular orbit at a height h = R above the surface of Earth, where R is the radius of Earth. The radius and mass of Earth are 6.4 x 10" m and 6.0 x 10" kg,...

W AutoSave Off S1b-Pendulum and Hookes Law 3-29-22 (1) . Saved to this PC . Search (Alt+Q) shemar tulloch ST X File Home Insert Draw Design Layout References Mailings Review View Help Comments Share...

A block with mass m = 6 . 6 kg is hung from a vertical spring. When the mA block with mass m = 5 . 2 kg is attached to two springs with spring constants kleft = 3 2 N / m and kright = 4 8 N / m . The...

Water witching, the practice of using the movements of a forked twig to locate underground water (or minerals), dates back over 400 years. Its first detailed description appears in Agricolas De re...

If La Bella advertises its pizza online and demand increases, the price of a pizza _______.

A test for job applicants. Your company gives a test of cognitive ability to job applicants before deciding whom to hire. Your boss has asked you to use company records to see if this test really...

=+c. Are the functions you wrote down homogeneous of degree 1? If the answer is no, could you find utility functions that are homogeneous of degree 1 and represent the same tastes? If the answer is...

In problem use a CAS or linear algebra software as an aid in finding the general solution of the given system. 1 -1.8 0 5.1 -1 3 X' = 1 -3 1 -3.1 4 -2.8 0 1.5 1 2. 2.

Verify that is a solution of the linear system for arbitrary constants c 1 and c 2 . By hand, draw a phase portrait of the system. x = )- C1 X C2.

In problem use the method of Example 2 to compute eAt for the coefficient matrix. Use (1) to find the general solution of the given system. X' = (;) -2

Computer Science II func. assignment #2 This is an example of a function where, (in the function) you read in 3 numbers, do a calculation, and return a value Write a C function that will: Determine...

The price of Microsolt (MSFT) today is $100 per share. MSFT has committed to make a $10.00 dividend payment in two years. The 0.0. risk-tree interest rate is flive percent. Assume there is no...

undefined Question 3. What happens on the balance sheets of banking system and the Fed, when the Fed make $ 75 million loan to First National Bank: (20 p.) a. Banking System (10 p.) Banking System...