As shown in following figure (a), a rightcircular cylinder partially filled with fluid is rotated with a constant angular velocity ω about a vertical y-axis through its center. The rotating fluid forms a surface of revolution S. To identify S, we first establish a coordinate system consisting of a vertical plane determined by the y-axis and an x-axis drawn perpendicular to the y-axis such that the point of intersection of the axes (the origin) is located at the lowest point on the surface S. We then seek a function y = f (x) that represents the curve C of intersection of the surface S and the vertical coordinate plane. Let the point P(x, y) denote the position of a particle of the rotating fluid of mass m in the coordinate plane. See the following figure (b).

(a) At P there is a reaction force of magnitude F due to the other particles of the fluid which is normal to the surface S. By Newton€™s second law the magnitude of the net force acting on the particle is mω²x. What is this force? Use the following figure (b) to discuss the nature and origin of the equations

Fcosθ = mg, Fsinθ = mω²x

(b) Use part (a) to find a first-order differential equation that defines the function y = f (x).

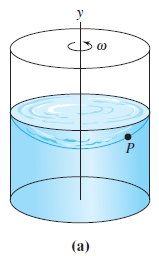
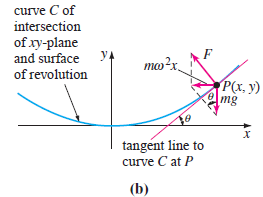
(a) curve C of intersection of xy-plane and surface y of revolution mwx, P(x. y) mg tangent line to curve C at P (b)