Question: Consider a mass-and-spring system containing two masses m 1 = 1 and m 2 = 1 whose displacement functions x(t) and y(t) satisfy the differential

Consider a mass-and-spring system containing two masses m₁ = 1 and m₂ = 1 whose displacement functions x(t) and y(t) satisfy the differential equations

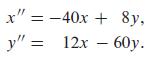
x"=-40x + 8y, y": = 12x - 60y.

(a) Describe the two fundamental modes of free oscillation of the system.

(b) Assume that the two masses start in motion with the initial conditions

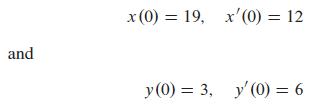
and are acted on by the same force, F₁(t) = F₂(t) = -195 cos 7t. Describe the resulting motion as a superposition of oscillations at three different frequencies.

x"=-40x + 8y, y": = 12x - 60y.

Step by Step Solution

★★★★★

3.39 Rating (146 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a The natural frequencies are 1 6 and 2 8 In mode 1 the two masses oscillate in the same di... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related First Course Differential Equations Questions!

In Problems 8 through 10 the indicated mass-and-spring system is set in motion from rest (x' 1 (0) = x' 2 (0) = 0) in its equilibrium position (x 1 (0) = x 2 (0) = 0) with the given external forces F...

In a television picture tube (a cathode ray tube) electrons are emitted with velocity vi from a source at the origin of coordinates. The initial velocities of different electrons make different...

Downloaded 02/28/15 to 132.174.255.3. Redistribution subject to SIAM license or copyright; see http://www.siam.org/journals/ojsa.php 15.7. Exercises 475 changes and we laugh no more. While...

Please write everything out for each part! 2-7. Species Accumulation and Transport within an Interface Accumulation and transport within an interface can be important for species that reside at phase...

The double spring A double spring consists of two springs, attached end - to - end, each with a point mass on the enc For this project, we will consider only the case where the two point masses are...

31. WRITING Two quadratic functions have graphs with |32. WRITING A quadratic function is increasing to the left vertices (2, 4) and (2, -3). Explain why you can not of * = 2 and decreasing to the...

1) Find all real solutions of: 4 2 2 x + x =3 2 x 4 + x23=0 4 2 2 2 x 2 x +3 x 3=0 x ( 21)=0 2 x 2 ( x 21)+ 3 ( 2 x2 +3 ) ( x 21 ) =0 ( 2 x2 +3 ) =0 2 2 x =3 3 x 2= 2 3 x= 2 3 x= i 2 2) Given the...

1. 3 2 Consider the function f(x) = x - 3x - 9x + 10, x (a) . Find the equation of the straight line passing through the maximum and minimum points of the graph y = f(x). (4) (b) Show that the point...

"Prisoners Rise, Rise, Rise!" Hip Hop as a Ciceronian Approach to Prison Protest and Community Care" explain a critical analysis summation on the chapter title assigned in relation to one of the key...

Match the assertions below with their appropriate test. You may use an assertion once, more than once, or not at all. More than one assertion may apply to a single test. (10 points) TESTS 1.Existence...

List three companies that are publicly traded in the US stock market but want that are not widely diverse, or they verified and identify future problems that the companies could incur.

What effect will this adjustment have on the accounting records? Unearned Revenue 3 , 3 0 0 Fees earned 3 , 3 0 0 Group of answer choices Increase net income Increase revenues reported for the period...

=+1. Wages are uniformly $25,900 for a five-day workweek, ending on Friday. The last payday of the year was Friday, June 27.

Reconsider the drive-through times (in seconds) for a Wendys and a Hot n Now restaurant from the previous question. a. The means for the two sets of times are 93.70 and 203.00 seconds. Which belongs...

Students collect the time (in seconds) for men and women to use the restroom at a mall in Michigan. The results are shown in the 6.1.23 histograms. a. One data set (male or female) has both the...

Statistics students were asked how many minutes of television they watched on the previous day. The results, in minutes, are shown in the 6.1.24 histograms, for the males in the top histogram and the...

A refrigerator used by a wholesale warehoose has a cost of $98,500, an estimated residual value of 56,500 , and an estimated useful life of 10 years. What is the amount of the annual depreciation...

Select the best answer. According to lan Redpath and Brian O'Sullivan, which of the following statements is correct regarding choice of entity? O A. Most clients should be transitioned to C...

Ling Company had the following transactions during 2011: - Sales of 9,000 on account - Collected 4,000 for services to be performed in 2012 - Paid 1,250 cash in salaries - Purchased airline tickets...