Determine whether Theorem 1.2.1 guarantees that the differential equation y' = (y 2 - 9) possesses a unique solution through the given point. 1. (1,

Determine whether Theorem 1.2.1 guarantees that the differential equation y' = ˆš(y²- 9) possesses a unique solution through the given point.

1. (1, 4)

2. (5, 3)

3. (2, 3)

4. (1, 1)

Theorem 1.2.1

Let R be a rectangular region in the xy-plane defined by a ‰¤ x ‰¤ b, c ‰¤ y ‰¤ d that contains the point (x₀, y₀) in its interior. If f (x, y) and Ï‘f /Ï‘y are continuous on R, then there exists some interval I₀: (x₀ h, x₀ + h), h > 0, contained in [a, b], and a unique function y(x), defined on I0, that is a solution of the initial value problem (2).

 

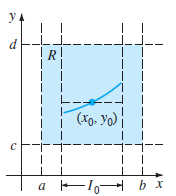
4 (- l