For each two-population system in Problems 26 through 34, first describe the type of x- and y-populations involved (exponential or logistic) and the nature of their interaction— competition, cooperation, or predation. Then find and characterize the system’s critical points (as to type and stability). Determine what nonzero x- and y-populations can coexist. Finally, construct a phase plane portrait that enables you to describe the long-term behavior of the two populations in terms of their initial populations x(0) and y(0).

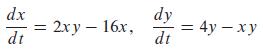
dx dt 2xy - 16x, dy dt = 4y - xy