If c ≠ 0, verify that the function defined by y(x) x/(cx - 1) (with the graph illustrated in Fig. 1.3.26) sat- isfies the differential equation x²y' + y² = 0 if x ≠ 1/c. Sketch a variety of such solution curves for different val- ues of c. Also, note the constant-valued function y(x) ≡ 0 that does not result from any choice of the constant c. Finally, determine (in terms of a and b) how many different solutions the initial value problem x²y' + y² = 0, y (a) = b has.

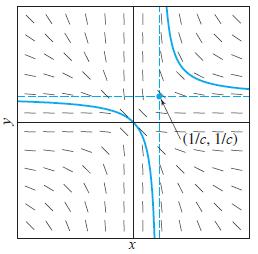
FIGURE 1.3.26. Slope field for x²y' + y² = 0 and graph of a solution y(x) = x/(cx - 1).

X (1/c, 1/c)