Question: Let S = {v 1 , v 2 , .... , v k } be a basis for the subspace W of R n .
Let S = {v1 , v2 , .... , vk} be a basis for the subspace W of Rn. Then a basis T for Rn that contains S can be found by applying the method of Example 5 to the vectors
v1 , v2 , ...... , vk , e1 , e 2, ...... , en.
Do this in Problems 17–20.
Find a basis T for R4 that contains the vectors v1 = (3 , 2 , 3 , 3) and v2 = (5 , 4 , 5 , 5).
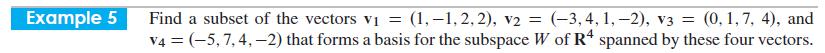
Example 5 Find a subset of the vectors v = (1,-1, 2, 2), v2 = (-3,4, 1,-2), V3 = (0, 1,7, 4), and V4 = (-5, 7, 4,-2) that forms a basis for the subspace W of R4 spanned by these four vectors.
Step by Step Solution
3.36 Rating (171 Votes )
There are 3 Steps involved in it
Basis vectors v ... View full answer

Get step-by-step solutions from verified subject matter experts


