Problems 28 through 30 develop a method of computing powers of a square matrix. If then show
Question:
Problems 28 through 30 develop a method of computing powers of a square matrix.
If
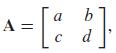
then show that
where I denotes the 2 x 2 identity matrix. Thus every 2 x 2 matrix A satisfies the equation
where det A = ad - bc denotes the determinant of the matrix A, and trace A denotes the sum of its diagonal elements. This result is the 2-dimensional case of the Cayley- Hamilton theorem of Section 6.3.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
adAadbcI a d 1 0 a da b ...View the full answer
Answered By
Ajeet Singh
Professional, Experienced, and Expert tutor who will provide speedy and to-the-point solutions.
I have been teaching students for 5 years now in different subjects and it's truly been one of the most rewarding experiences of my life.
I have also done one-to-one tutoring with 100+ students and help them achieve great subject knowledge.
I have expertise in computer subjects like C++, C, Java, and Python programming and other computer Science related fields.
Many of my student's parents message me that your lessons improved their children's grades and this is the best only thing you want as a teacher. I have done plenty of studying and lots of learning on many exciting and challenging topics. All these experiences have influenced my decision to take on the teaching role in various capacities. As a tutor, I am looking forward to getting to understand your needs and helping you achieve your academic goals. I'm highly flexible and contactable. I am available to work on short notice since I only prefer to work with very small and select groups of students.
7+ Reviews
15+ Question Solved
Related Book For 
Differential Equations And Linear Algebra
ISBN: 9780134497181
4th Edition
Authors: C. Edwards, David Penney, David Calvis
Question Posted:
