Question: Problems 43 through 46 concern the differential equation where k is a constant. (a) If k is a constant, show that a general (one-parameter) solution

Problems 43 through 46 concern the differential equation

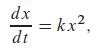
dx dt = kx2,

where k is a constant.

(a) If k is a constant, show that a general (one-parameter) solution of the differential equation is given by x(t) = 1/(C - k t), where C is an arbitrary constant.(b) Determine by inspection a solution of the initial value problem x' = kx², x(0) = 0.

dx dt = kx2,

Step by Step Solution

★★★★★

3.44 Rating (179 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a We need only substitute xt 1C kt in bot... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related First Course Differential Equations Questions!

The position vector r describes the path of an object moving in space. (a) Find the velocity vector, speed, and acceleration vector of the object. (b) Evaluate the velocity vector and acceleration...

In Exercises at the indicated point find (a) The slope of the curve, (b) An equation of the tangent, and (c) An equation of the normal. (d) Then draw a graph of the curve, tangent line, and normal...

234/90Th undergoes beta decay. What is the atomic number of theresulting element? Express your answer numerically as an integer. Z = ?

Problems 43 through 46 concern the differential equation where k is a constant. Suppose a population P of rodents satisfies the differential equation dP/dt = kP 2 . Initially, there are P(0) = 2...

A container of hot liquid is placed in a freezer that is kept at a constant temperature of 20F. The initial temperature of the liquid is 160F. After 5 minutes, the liquid's temperature is 60F. (a)...

Answer the following problems here are the instructions. Write the letter of the answer which is correct and if the answer is not on the given choices, please write INCORRECT As well as write the...

Problem 1. Solow model: balanced growth path and convergence Consider the standard Solow model, where the production function is the Cobb-Douglas function Y = K (AL)*, where Yis GDP, K is capital. L...

17. Consider the nonlinear differential equation dy /dt = y2. (a) Show that y;(t) = 1/(1 t) is a solution. (b) Show that y>() = 2/(1 t) is not a solution. () Why don't these two facts contradict the...

Why do most firms employ a combination of departmentalization bases?

Why may the Sarbanes-Oxley Act of 2002 be regarded as one of the most controversial pieces of corporate legislation in recent history?

why might some very small businesses choose to use the cash basis

To what extent has the researcher adhered to the criteria that define quality for the quantitative portion of the study?

Answer the fallowing questions/or the differential equations of Problems, using the direction fields given as a guide. (a) Are there any constant solutions? If so, what are they? (b) Are there points...

The simplest case of the logistic model is represented by the DE dy/dt = ky( I - y). Where k > 0 is the growth rate constant Draw a direction field for this equation when k = I. Find the constant...

When a lint-order DE has the form y' = f(y), so the right-band side doesn't depend oo t, the equation is called autonomous (which means independent of time). The logistic equation y' = ky(1 - y) in...

On January 3, 2018, Nimble Delivery Service purchased a truck at a cost of $80,000. Before placing the truck in service, Nimble spent $3,000 painting it, $500 replacing tires, and S8,500 overhauling...

The Sweetwater Candy Company would like to buy a new machine that would automatically dip chocolates. The dipping operation currently is done largely by hand. The machine the company is considering...

Bill Darby started Darby Company on January 1 , Year 1 . The company experienced the following events during its first year of operation: 1. Earned $1,100 of cash revenue. 2. Borrowed $2,000 cash...