The system in Problem 19, like the system in (2), canbe solved with no advanced knowledge. Solve for x(t) and y(t) and compare their graphs with your sketches in Problem 19. Determine the limiting values of x(t) and y(t) as t †’ ˆž. Explain why the answer to the last question makes intuitive sense.

Data from problem 19

Suppose compartments A and B shown in the following figure are fi­lled with fluidsand are separated by a permeable membrane. The fi­gure is a compartmental representation of the exterior and interior of a cell. Suppose, too, that a nutrient necessary for cell growth passes through the membrane. A model for the concentrations x(t) and y(t) of the nutrient in compartments A and B, respectively, at time t is given by the linear system of differential equations

dx/dt = k/V_A (y - x)

dy/dt = k/V_B (x - y) ,

where V_A and V_B are the volumes of the compartments, and k > 0 is a permeability factor. Let x(0) = x₀ and y(0) = y₀ denote the initial concentrations of the nutrient. Solely on the basis of the equations in the system and the assumption x₀ > y₀ > 0, sketch, on the sameset of coordinate axes, possible solution curves of the system. Explain your reasoning. Discuss the behavior of the solutions over a long period of time.

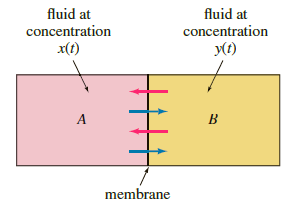
fluid at fluid at concentration ) concentration x(t) A membrane