To solve the two equations in (10) for the values of k and M, begin by solving the first equation for the quantity x = e^-50kM and the second equation for x² = e^-100kM. Upon equating the two resulting expressions for x² in terms of M, you get an equation that is readily solved for M. With M now known, either of the original equations is readily solved for k. This technique can be used to “fit” the logistic equation to any three population values P₀, P₁, and P₂ corresponding to equally spaced times t₀ = 0, t₁, and t₂ = 2t₁.

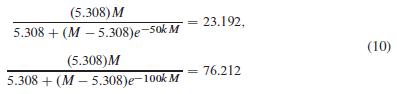
(5.308) M 5.308 +(M-5.308)e-50k M (5.308)M 5.308+ (M-5.308)e-100k M 23.192, = 76.212 (10)