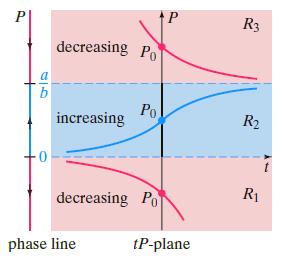
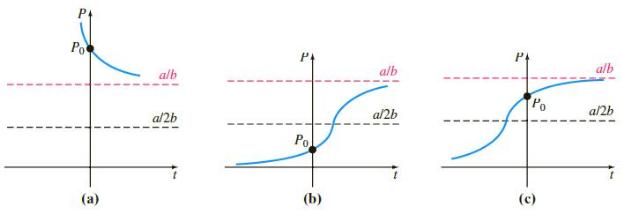
With the identifi­cations a = r, b = r/K, and a/b = K, Figures (1) and (2) show that the logistic population model, (3) of Section 3.2, predicts that for an initial population P₀, 0, K, regardless of how small P₀is, the population increases over time but does not surpass the carrying capacity K. Also, for P₀> K the same model predicts that a population cannot sustain itself over time, so it decreases but yet never falls below the carrying capacity K of the ecosystem. The American ecologist Warder Clyde Allee (1885€“1955) showed that by depleting certain ­fisheries beyond a certain level, the ­fish population never recovers. How would you modify the differential equation (3) to describe a population P that has these same two characteristics of (3) but additionally has a threshold level A

(1)

(2)

R3 decreasing Po a b Po increasing R2 decreasing Po R1 phase line tP-plane