Using the integral relations from Problem 19.17, and assuming the velocity and temperature profiles of the form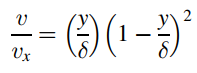 

and 

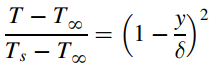
where δ is the thickness of both the hydrodynamic and thermal boundary layers, show that the solution in terms of δ and v_x from each integral equation reduce to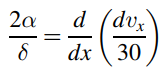 and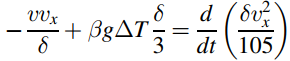

Next, assuming that both δ and v_x vary with x according to

δ = Ax^α         and        v_x = Bx^b

show that the resulting expression for d becomes
δ/x = 3.94 Pr^-1/2 (Pr + 0.953)^1/4 Gr_x^-1/4

and that the local Nusselt number is
Nu_x = 0.508    Pr^-1/2 (Pr + 0.953)^-1/4 Gr_x^1/4

Data From Problem 19.17

Show that, for the case of natural convection adjacent to a plane vertical wall, the appropriate integral equations for the hydrodynamic and thermal boundary layers are 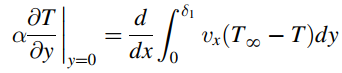 and

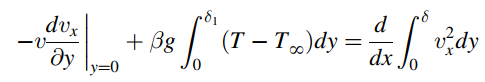
2 8) Vx - 00 Ts- T. 8)