Question: Consider a function f(t) which is continuous and bounded on [0, t]. Prove integration by parts, i.e. | f(t)dX(t) = f(t)X(t) -| X(t)df(t).

Consider a function f(t) which is continuous and bounded on [0, t]. Prove integration by parts, i.e.

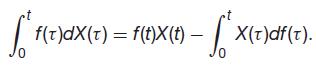
| f(t)dX(t) = f(t)X(t) – -| X(t)df(t).

| f(t)dX(t) = f(t)X(t) -| X(t)df(t).

Step by Step Solution

★★★★★

3.27 Rating (168 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

The decision of whether or not to move your 401k to bo... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Introduces Quantitative Finance Questions!

Q:

Suppose that f: (0, ) R is continuous and bounded and that £{f} exists at some a (0, ). Let a) Prove that for all N N. b) Prove that the integral «0 e-(s-a)t(ɸ)(t)dt...

Q:

Give an example of a function f which satisfies the intermediate-value property on a closed and bounded interval [a, b] but is not continuous on a, 6). () Give an example of a function f which is...

Q:

The continuous function f f is defined for 4x4 4 x 4 . The graph of f f , shown above, consists of two line segments and portions of three parabolas. The graph has horizontal tangents at x=12,...

Q:

(a) Consider the function f : R - R defined by 2 if x 0. (i) Prove that f is discontinuous at 0. [3] (ii) Using only the definition of continuity, prove that f is continuous at every c 0. [5] (b)...

Q:

Consider the function f ( x) = tan -1( tan x ). Then f (0) =f (x) =0. Your professor claims that by the Mean Value Theorem, there is a number con (0, x) such that f(c) =0. (a) Prove your professor...

Q:

Math 104A Homework #3 Instructor: Lihui Chai General Instructions: Please write your homework papers neatly. You need to turn in both full printouts of your codes and the appropriate runs you made....

Q:

I am really desperate for someone to answer all 4 parts of this question (d, e, f, and g) (I have already posted this question twice and no one has answered all 4 parts sufficiently). This is due in...

Q:

These are questions of Math 1B, which are calculus problems. 19. Evaluate: a f eSxl dx b [xi2d): c f x(x:+8) d f (1+:x)3 dx e. f x cos(5x) dx f fflgzydy g. Use substitution, followed by integration...

Q:

MATH 1P97, WINTER 2016-17 ASSIGNMENT 3 Due Date: Monday March 6, 2017 at 11:59 p.m. Home assignments are individual submissions. While students are encouraged to work together, they cannot submit...

Q:

5) Calc: ; f(x) = 4 - |x] 6) Calc: f(x) = tan x 6- 7) 8) Given the areas, determine the integrals. (8 - 2x) dx ['s() dx - 10 and [ f()ax = 3 evaluate ca ) [ 35() dx. 9) Given the areas, Determine the...

Q:

The following data were taken from the financial statements of Gates Inc. for the current fiscal year. Property, plant, and equipment (net) Liabilities: $1,470,600 Current liabilities $164,000 Note...

Q:

Qn. B2 (a) State Dalton's Law of Additive Pressure. (b) A room contains moist air comprising of 0.3 moles of oxygen, 0.6 moles of nitrogen and 0.1 moles of water vapor at room temperature (25 C) and...

Q:

A plane electromagnetic wave with a single frequency moves in vacuum in the positive x direction. Its amplitude is uniform over the y z plane. As the wave moves, its intensity: increases. decreases....

Q:

How do you segment your market? Who is your PTA? Who are your STAs?

Q:

Using a decay factor of 0.95, calculate the mean, sample variance, and sample standard deviation of the following series. Assume t = 7 is the most recent data point and use all eight points: x 0 11 1...

Q:

Given the probability density function for a random variable X, find the variance of X. f(x) = X 18 for 0 x 6

Q:

Calculate the population mean, standard deviation, and kurtosis for each of the following two series: Series #1 Series #2 -23 -17 -7 -17 7 17 23 17

Q:

Q.No.2 (5 marks) Three independent projects, each of which requires a RS 5 million investment are being considered for investment purpose by Sona Tea Company. The cost of capital and estimated...

Q:

Recently, a nurse commented that when a patient calls the medical advice line claiming to have the flu, the chance that he or she truly has the flu (and not just a nasty cold) is only about 4%. Of...

Q:

A forward contract with a settlement date at time T is issued based on an underlying asset with a current market price of B. The annualised risk-free force of interest applying over the term of the...