The solution to the initial value problem for the diffusion equation is unique (given certain constraints on the behavior, it must be sufficiently smooth and decay sufficiently fast at infinity). This can be shown as follows:

Suppose that there are two solutions u₁(x, τ) and u₂(x, τ ) to the problem

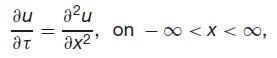
with
u(x, 0) = u₀(x).
Set v(x, τ ) = u₁ − u₂. This is a solution of the equation with v(x, 0) = 0. Consider

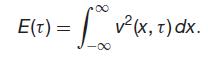
Show that

E(τ ) ≥ 0, E(0) = 0,

and integrate by parts to find that

dE/dτ ≤ 0.

Hence show that E(τ) ≡ 0 and, consequently, u₁(x, τ ) ≡ u₂(x, τ ).

au a?u on - 00 < X < 00, ax2'