A two degree of freedom spring-mass-damper system is shown in Fig. P4.7. For harmonic free vibration, complete the following  if \(k_{1}=2 \times 10^{5} \mathrm{~N} / \mathrm{m}\), \(c_{1}=60 \mathrm{~N}-\mathrm{s} / \mathrm{m}, m_{1}=2.5 \mathrm{~kg}, k_{2}=5.5 \times 10^{4} \mathrm{~N} / \mathrm{m}, c_{2}=16.5 \mathrm{~N}-\mathrm{s} / \mathrm{m}\), and \(m_{2}=1.2 \mathrm{~kg}\).
(a) Verify that proportional damping exists.
(b) Define the modal matrix and determine the modal mass, stiffness, and damping matrices. Normalize the mode shapes to coordinate \(x_{2}\).

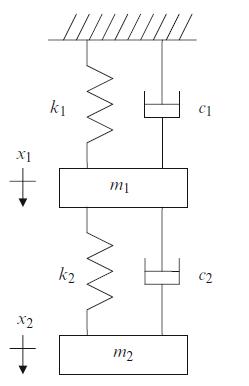
Fig. P4.7 Two degree of freedom spring-mass-damper system under free vibration.

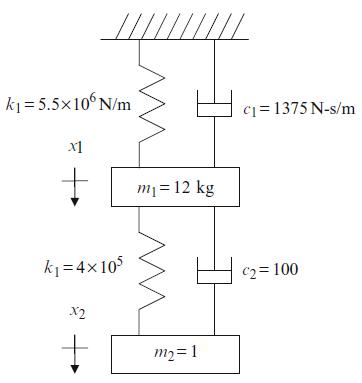
Fig. P4.8 Two degree of freedom spring-mass system.

1x k1 mi /// k2 C2 x2 m2