Consider a fixed-free beam. The general solution to the equation of motion can be written as \(Y(x)=A \cos (\lambda x)+B \sin (\lambda x)+C \cosh (\lambda x)+D \sinh (\lambda x)\). To determine the four coefficients, \(A\) through \(D\), four boundary conditions are required. Write the four boundary conditions (in the table) as a function of \(x\) and \(y\) for the beam shown in Fig. P8.3.

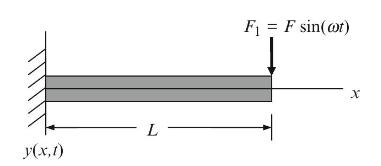
Fig. P8.3 Fixed-free beam model.

y(x,1) L F = F sin(cot) x