Let p be an odd prime. A number a ? Z^*_p is a?quadratic residue?if the equation?x² =?a (mod?p)?has a solution for the unknown?x.

a.?Show that there are exactly?(p???1)/2?quadratic residues, modulo?p.

b.?If?p?is prime, we define the?Legendre symbol?(a/p?), for?a????^*_p, to be?1?if?a?is a?quadratic residue modulo?p?and???1?otherwise. Prove that if?a????^*_p, then

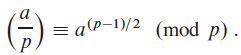
Give an efficient algorithm that determines whether a given number a is a quadratic residue modulo p. Analyze the efficiency of your algorithm.

c.?Prove that if?p?is a prime of the form?4k?+?3?and?a?is a quadratic residue in??^*_p,?then?a^k?+?1 mod?p?is a square root of?a, modulo?p. How much time is required?to find the square root of a quadratic residue?a?modulo?p?

d.?Describe an efficient randomized algorithm for finding a nonquadratic residue, modulo an arbitrary prime?p, that is, a member of??^*_p that is not a quadratic residue. How many arithmetic operations does your algorithm require on average?

(-1)2 (mod p).