Show that splitting an edge in a flow network yields an equivalent network. More formally, suppose that flow network G contains edge (u, ν), and we create a new flow network G€² by creating a new vertex x and replacing (u, ν) by new edges (u, x) and (x, ν) with c(u, x) = c(x, ν) = c(u, ν). Show that a maximum flow in G€² has the same value as a maximum flow in G.

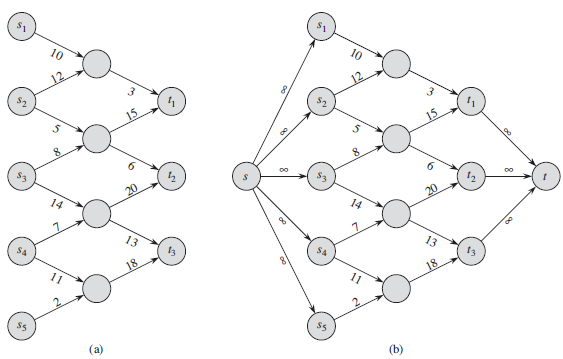
Figure 26.3 Converting a multiple-source, multiple-sink maximum-flow problem into a problem with a single source and a single sink. 

S1 10 10 12 15 S2 15 8. 8. 00 20 00 20 14 13 S4 13 13 18 S4 13 18 S5 (a) (b)