The chirp transform of a vector a = (a 0 , a 1 , . . .
Question:
The chirp transform of a vector a = (a0, a1, . . . ,an-1) is the vector y= (y0, y1, . . . ,yn-1), where yk = Σn-1j=0?aj zkj and z is any complex number. The DFT is therefore a special case of the chirp transform, obtained by taking z = ωn. Show how to evaluate the chirp transform in time?O(nlgn)?for any complex number?. Use the equation
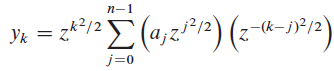
to view the chirp transform as a convolution.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
The chirp transform of a vector a can be viewed as a convolution using the equation yk ...View the full answer
Answered By
Dulal Roy
As a tutor, I have gained extensive hands-on experience working with students one-on-one and in small group settings. I have developed the ability to effectively assess my students' strengths and weaknesses, and to customize my teaching approach to meet their individual needs.
I am proficient at breaking down complex concepts into simpler, more digestible pieces, and at using a variety of teaching methods (such as visual aids, examples, and interactive exercises) to engage my students and help them understand and retain the material.
I have also gained a lot of experience in providing feedback and guidance to my students, helping them to develop their problem-solving skills and to become more independent learners. Overall, my hands-on experience as a tutor has given me a deep understanding of how to effectively support and encourage students in their learning journey.
0 Reviews
10+ Question Solved
Related Book For 
Introduction to Algorithms
ISBN: 978-0262033848
3rd edition
Authors: Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest
Question Posted:
