We can generalize the 1-dimensional discrete Fourier transform defined by equation (30.8) to d dimensions. The input is a d-dimensional array A = (a_j1,j₂,...,j_d)?whose dimensions are?n₁, n₂, . . . ,n_d, where?n₁n₂ . . .?n_d =?n. We define the?d-dimensional discrete Fourier transform by the equation

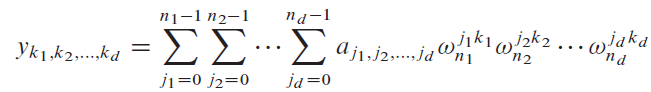
for

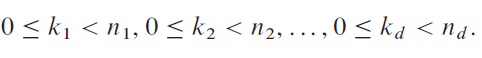
a. Show that we can compute a d-dimensional DFT by computing 1-dimensional DFTs on each dimension in turn. That is, we first compute n/n₁ separate?1-dimensional DFTs along dimension?1. Then, using the result of the DFTs along dimension?1?as the input, we compute?n/n₂ separate?1-dimensional DFTs along dimension?2. Using this result as the input, we compute?n/n₃ separate?1-dimensional DFTs along dimension?3, and so on, through dimension?d.

b.?Show that the ordering of dimensions does not matter, so that we can compute a?d-dimensional DFT by computing the?1-dimensional DFTs in any order of the?d?dimensions.

c. Show that if we compute each 1-dimensional DFT by computing the fast Fourier transform, the total time to compute a d-dimensional DFT is O(n lg n), independent of d.

0 < k1 < n1, 0 < k2 < n2, .., 0 < ka < na.