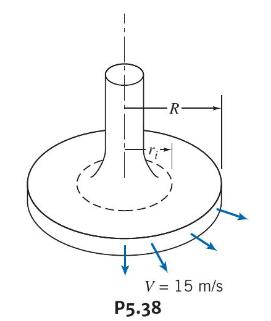
Consider the low-speed flow of air between parallel disks as shown. Assume that the flow is incompressible and inviscid, and that the velocity is purely radial and uniform at any section. The flow speed is \(V=15 \mathrm{~m} / \mathrm{s}\) at \(R=75 \mathrm{~mm}\). Simplify the continuity equation to a form applicable to this flow field. Show that a general expression for the velocity field is \(\vec{V}=V(R / r) \hat{e}_{r}\) for \(r_{i} \leq r \leq R\). Calculate the acceleration of a fluid particle at the locations \(r=r_{i}\) and \(r=R\).

Transcribed Image Text:

R- V = 15 m/s P5.38