A random variable X has distribution function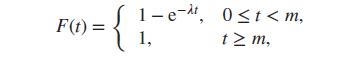

where ???? and m are positive constants.
(i) Identify the point(s) at which F has jumps.
(ii) Find the density function associated with the continuous part of this distribution.
(iii) Show that the expectation of X is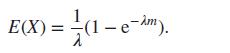

11. An insurance contract with deductible amount a and retention level b (with 0

b) entails the following agreement: Let Y be the size of the loss incurred to the insured. If Y ≤

a, the customer pays the full amount of this loss, while if a

b, the customer is responsible for the amount a and the company pays the difference Y −

a. Finally, for Y >

b, the company pays the amount b −

a. The size of the customer’s loss Y is a continuous random variable with distribution function FY and density fY .
(i) Verify that the distribution function F of the amount X that the company pays for a claim is given by the expression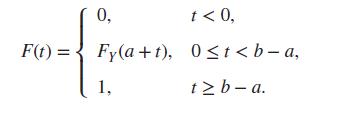

(ii) Show that the density, f2, for the continuous part of F is f2(x) = f (a + x), 0

a, while the probability function associated with the discrete part of F is given by f1(0) = FY (a), f1(b −

a) = 1 − FY (b).

(iii) Prove that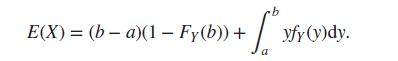

(iv) Give numerical answers to Parts (ii) and (iii) when Y has the density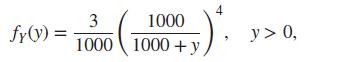

while a and b can be determined by knowing that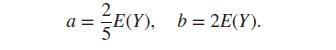

1-et, 0