Consider the events A1, A2,, An defined in a sample space . Show that the probability that none of them appear is equal to where

Consider the events A1, A2,…, An defined in a sample space Ω. Show that the probability that none of them appear is equal to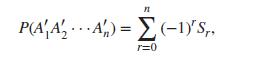

where S1, S2,…, Sn are the sums defined earlier in Proposition 1.10, and S0 = 1.
Application: For n = 3 assume that P(Ai) = 1∕3 for i = 1, 2, 3. Moreover, assume that P(AiAj) = 1∕9 for any i ≠ j, and P(A1A2A3) = 1∕27. Then, show that P(A′
1A′
2A′
3) = P(A′
1)P(A′
2)P(A′
3).

n P(AAA)=(-1)'S, r=0