Question: Consider the likelihood function f (x1, . . . , xn|) and suppose that is uniformly distributed over some interval (a, b). The posterior

Consider the likelihood function f (x1, . . . , xn|θ) and suppose that θ is uniformly distributed over some interval

(a, b). The posterior density of θ given X1, . . . , Xn equals

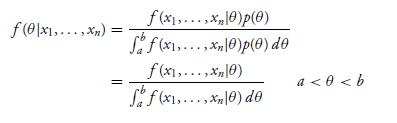
f(0|x1,...,xn) = f(xx)p(0) ff(x1,...,xn)p(0) de f(x1,...,x10) a

f(0|x1,...,xn) = f(xx)p(0) ff(x1,...,xn)p(0) de f(x1,...,x10) a

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Introduction To Probability Statistics Questions!

Q:

Answer all the questions accordingly Problem 1 Suppose a sequence of random variables is generated as follows. Let X] ~ uniform(0, 1), and X2 X] ~ uniform(X1, 1). In general, let Xxtil(X1, ..., Xx) ~...

Q:

Please answer this question 1. (30 points) Let X1, .... Xn be i.i.d. Exponential(1/0) random variables with common probability density function (pdf) f(x|0) = exp (-), x>0, 0>0. (a) (8 points) Derive...

Q:

A set of random variables, X1, X2, X3, Xn, are independent and each uniformly distributed over ( 0, 1). (a) Find the probability density function of Z = max(X1, X2 Xn). (b) With defined as in part...

Q:

Question Four Part I Consider a random sample X = (X1, . .., Xn ) of size n = 10 from a normal distribution N(0, 10). Note that the density function of a N(u, o?) is given by f (x| M, o ) = - 1 e 20I...

Q:

please help!!! Let X1, ..., Xn be a collection of random variables with joint density px (1, . .., In) and let g : R" - R" be an invertible function from (X1, . .., In) to (y1, . .., yn) like Yi =...

Q:

Consider a set of samples {x1, x2,...,xN} that are independent and identically distributed (i.i.d.) according to a Gaussian distribution p(xi) = G (x;; , o), where i = 1, 2,..., N. Recall that the...

Q:

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

Q:

Exercises Chapter 2 2.1 Marginal and conditional probability: The social mobility data from Section 2.5 gives a joint probability distribution on (Y1 , Y2 )= (father's occupation, son's occupation)....

Q:

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

Q:

1. (60 pts True/False. Indicate whether the statement is true or false. If the statement is false, present an explanation or counterexample. (No explanation necessary for each true statement.) (2...

Q:

Match the following terms with the appropriate definitions. ____ JIT ____ CIC ____ Supply chain efficiency ____ SCM ____ Supply chain ____ VMI ____ Supply chain visibility ____ CAM ____ CRM ____ RFID

Q:

Y = 3x Determine the slope and the y-intercept. Then use the slope and the y-intercept to graph the equation by hand.

Q:

1 2 - 3 Explain why net operating working capital is included in a capital budgeting analysis and how it is recovered at the end of a project s life.

Q:

The lack of innovation and entrepreneurial focus at American Express (AmEx) may be because of hubris, inertia, and a lack of capability. The firms performance in 2014 was not, by any means, what...

Q:

Cars pass a certain street location according to a Poisson process with rate . A woman who wants to cross the street at that location waits until she can see that no cars will come by in the next T...

Q:

Customers arrive at a two-server service station according to a Poisson process with rate . Whenever a new customer arrives, any customer that is in the system immediately departs. A new arrival...

Q:

Customers arrive to a single server system according to a Poisson process with rate . An arrival that finds the server idle immediately begins service; an arrival that finds the server busy waits....

Q:

2 (10 points) A life insurance policy that pays dividends is known as a participating policy. a. Identify the sources from which dividends can be paid. b. List the various dividend options in a...

Q:

Chapter 9 Homework 8.34 3 points Exchange Corp. is a company that acts as a facilitator in tax-favored real estate swaps. Such swaps, know as 1031 exchanges, permit participants to avoid some or all...

Q:

Marinette Company makes several products, including canoes. The company has been experiencing losses from its canoe segment and is considering dropping that product line. The following information is...