Consider the sample space S = [0, 1] with a probability measure that is uniform on this space, i.e.,

Define the sequence {X_n, n = 1, 2,⋯} as follows: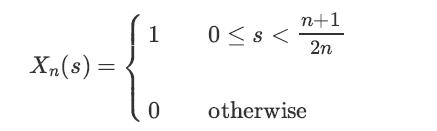

Also, define the random variable X on this sample space as follows: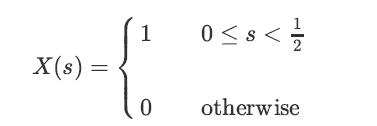

Show that X_n ^a.s.→ X.

P([a, b])=b-a, for all 0 < a < b < 1.