For large values of a positive integer n, an approximation which is often used for its factorial,

Question:

For large values of a positive integer n, an approximation which is often used for its factorial, n!, is the following, known as Stirling’s formula:

Here, the symbol ∼ means that the ratio of the two sides tends to 1 as n → ∞, so that the formula can also be written in the form image text in transcribed

Calculate the values of the quantity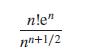 image text in transcribed

for n = 20, 30, 40, 50, 60, 80,100, 120,150 and plot these points against n on a graph.
Check that even for modest values of n, this gets very close to √
2π.