Question: Let W(t) be a standard Brownian motion. Let a > 0. Define Ta as the first time that W(t) = a. That is a. Show

Let W(t) be a standard Brownian motion. Let a > 0. Define Ta as the first time that W(t) = a. That isTa = min{t: W(t) = a}.

a. Show that for any t ≥ 0, we haveP(W(t) a) = P(W(t) aTa t)P(Ta t).

b. Using Part (a), show thatP(Ta t)=21-0 a (+7)] t

c. Using Part (b), show that the PDF of Ta is given by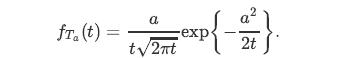fr. (t) = a t/2t p{-} exp 2t

By symmetry of Brownian motion, we conclude that for any a ≠ 0, we have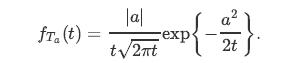fra (t) = lal t2t exp 2t

Ta = min{t: W(t) = a}.

Step by Step Solution

★★★★★

3.38 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Introduction To Probability Statistics Questions!

Q:

When are employees more likely to make claims of unlawful discrimination during the performance management process?

Q:

A private startup company has just gone public. It is not expected to pay any dividends for the first 2 years. It is then expected to pay dividends of $13 per share with 10% growth for 4 years. After...

Q:

Samara Co. Manufactures chairs for use in patios & gardens. Because of the seasonality business of Samara managers prepare annual budget for the company. The companys controller Ahmed Ali is...

Q:

Using a search engine or database, conduct research including references; taking into consideration the following: Diversity Diversity Management Culture ?

Q:

Answer all questions with detailed explanation Question A derivatives trader is modelling the volatility of an equity index using the following discrete-time model: Model 1: Of = 0.12+0.40,_1+0.056 ,...

Q:

Question 4 Let B ( t ) be a standard Brownian motion starting at B ( 0 ) = 0 . Define the process x ( t ) as: x ( t ) = B ( t ) 2 - t ( a ) Show that x ( t ) is a martingale with respect to the...

Q:

The one-factor Hull-White model follows the stochastic differential equation dr = (0(t) - Yri)dt + odW, where re is the short rate, W, a standard Brownian motion, and o > 0 are constants and 6 a...

Q:

A government subsidised a new factory in a rural area to create jobs. It also provided training courses at a college. Objectors claimed the development would destroy an area of natural beauty. What...

Q:

Exercise 7.20 Let \(\left(B_{t}ight)_{t \in \mathbb{R}_{+}}\)be a standard Brownian motion generating a filtration \(\left(\mathcal{F}_{t}ight)_{t \in \mathbb{R}_{+}}\). Recall that for \(f \in...

Q:

20 3 points] Let B be a one-dimensional standard Brownian motion de- fined on an underlying probability space (0, F, P). Let B and X be the processes defined by B(t) = B(t) + 1 and X(t) = B(t +1),...

Q:

20. [3 points] Let B be a one-dimensional standard Brownian motion de- fined on an underlying probability space (S, F, P). Let B and X be the processes defined by B(t) = B(t) + 1 and X(t) = B(t+1),...

Q:

A hiker walks 15 km towards the north then 16 km towards the east then 15 km towards the north. How far away and in which direction is the hiker with reference to the starting point? Pick ONE option...

Q:

Transpacific Airlines (TPA) budgeted 80 million passenger-miles, or 5 percent of the total market for the year just completed at a contribution margin of 40 cents per mile. The budgeted variable cost...

Q:

How to structure a keep-or-drop product-line problem with complementary effects?

Q:

18.3. Multiple poles Prove that the amplitude S11 of the fundamental particle cannot have higher-order poles by showing that the resonance angle of two heavier masses is larger than 2/3. This makes...

Q:

Identify the various sources of revenues in the federal budget.

Q:

A U.S.-based multinational corporation (MNC) sold some equipment to a British firm today and will receive 1,000,000 from the British firm one month from today. Todays spot rate is $1.12/. The MNC is...

Q:

A U.S.-based multinational corporation (MNC) purchased equipment from a British firm today and must pay them 1,000,000 one month from today. The MNC is certain the spot rate will be $1.10/ one month...

Q:

Five years ago you purchased an 8% coupon bond for $975. Today you sold the bond for $1,000. Use the yield-to-maturity method to compute the rate of return on your bond investment. (Round your...

Q:

amys service center received s 120-day 6% nitr for $40,000 dated april 12 from a customer on account

Q:

Your investment club has only two stocks in its portfolio. $45,000 is invested in a stock with a beta of 0.7, and $70,000 is invested in a stock with a beta of 1.2. What is the portfolio's beta? Do...