Let X 1 , X 2 , X 3 , , Xn be a random sample from a distribution with mean EX i , and variance Var(X i ) 2 Consider the following two estimators for Find MSE( 1 ) and MSE( 2 ) and show that for n 1, we have 1 n X1 X 2 , X X X Xn n

Question: Let X 1 , X 2 , X 3 , . . ., Xn be a random sample from a distribution with mean EX i

Let X₁, X₂, X₃, . . ., Xn be a random sample from a distribution with mean EX_i = θ, and variance Var(X_i) = σ². Consider the following two estimators for θ: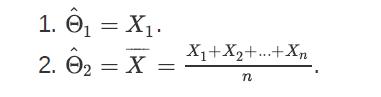 1. n = X1. X. 2. , = X X+X+...+Xn n

Find MSE(^Θ₁) and MSE(^Θ₂) and show that for n > 1, we have MSE() > MSE().

1. n = X1. X. 2. , = X X+X+...+Xn n

Step by Step Solution

★★★★★

3.45 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

We have MSE E 0 To find MSE we can write MSE EX EX VarX ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Introduction To Probability Statistics Questions!

Let X1,.., Xn be a random sample from a population with mean Î¼ and variance Ï2. (a) Show that the estimator is an unbiased estimator of Î¼ if (b) Among all unbiased...

Let X1, X2,..., Xn be a random sample from a uniform distribution on the interval [0, Ã¸], so that Then if Y = max (Xi), it can be shown that the rv U = Y/Ã¸ has density...

Let X1, X2, . . . , Xn be a random sample from a gamma distribution with known and with = 1/. Say has a prior pdf that is gamma with parameters 0 and 0, so that the prior mean is 00. (a) Find the...

Please help with this question. Please provide all steps and calculations. Please don't use answers from other websites, I looked at them and didn't understand them. Thank you Problem 7 Let X 1, X 2,...

Recall: k) In addition to many other wonderful services it provides, CourseCheggHero benets nancially from its customers' inability and/ or unwillingness to do their homework. Suppose that the time...

\f 1 Let X 1 , X 2 ,....., X n is a random sample from a normal distribution with mean and variance 02 known. Then probabilily density function 1 x i 2 0 1 f xi 2 e , xi , 0, 0 2 By def, Likelihood...

STA5326 - Mathematical Statistics - II Homework # 3 1. If X 1 , X 2 ,..., X n is a random sample of size n from N ( , 2 ), , show that n n n 2 2 X j , X j or X , X j = = j 1 j 1 =j 1 is a sufficient...

Q6. Suppose that X =61 + 52, where 1 N N(6,1), 52 ~ N()\\6', A2), and 1 and 52 are in- dependent. Here, A 2 1 is a given constant, and 6 is a unknown parameter. (iv) Let X 1, X 2, - - - ,Xn be an...

9. Let X and Y be independent and identically distributed random variables with mean / and variance oz. Find the following: (a) E[(X + 2) 2] (b) Var(3X + 4) (c) E[(X - Y) 2] (d) Cov{ (X + Y), (X - Y)...

1. Let q; > 0 be a population parameter, and let X l , X 2, , X n be a random sample from a distribution with probability density function 2 105311) : 2 9K A, , x> 0. zero otherwise. m Recall: W = X2...

Your pro-forma income statement shows sales of $1,000,000, cost of goods sold as $500,000, depreciation expense of $100,000, and taxes of $160,000 due to a tax rate of 40%. What are your pro-forma...

State 5 advantages and disadvantages of floating charges in a company?

What is the bid - ask spread if the current ask prices for DEF are $ 8 . 0 0 and $ 8 . 1 7 and current bid prices are $ 7 . 7 8 and $ 7 . 9 3 ? $ 0 . 0 7 $ 0 . 2 4 $ 0 . 3 9 $ 0 . 2 2

5. Assume that as their leader, you wanted to influence minimum wage earners in an order-fulfillment center to work faster. Which one or two influence tactics are likely to be effective?

Check whether the following can define probability distributions and explain your answers. (a) $f(x)=\frac{1}{4}$ for $x=10,11,12,13$ (b) $f(x)=\frac{2 x}{5}$ for $x=0,1,2,3,4,5$ (c)...

Given that $f(x)=\frac{k}{2^{x}}$ is a probability distribution for a random variable that can take on the values $x=$ $0,1,2,3$, and 4 , find $k$.

With reference to Exercise 4.5, find an expression for the distribution function $F(x)$ of the random variable. Data From Exercise 4.5 k 4.5 Given that f(x): = is a probability distribution for 2x...

Effect of Stock Split Gino's Restaurant Corporation wholesales ovens and ranges to restaurants throughout the Midwest. Gino's Restaurant Corporation, which had 57,000 shares of common stock...

Factors common to the bond rating agencies risk assessment are the economy and a governments debts. True False

QUESTION6 Partially correct Mark 3.33 out of 5.00 P Flag question Interpreting Disclosure on Employee Stock Options Intel Corporation reported the following in its 2015 10-K report. Share-Based...