Question: Let X 2 , X 3 , X 4 , be a sequence of random variables such that Show that X n converges in

Let X2, X3, X4, ⋯ be a sequence of random variables such that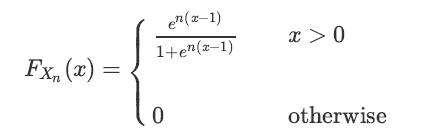Fx, (x) = en(x-1) 1+en (2-1) 0 x>0 otherwise

Show that Xn converges in distribution to X = 1.

Fx, (x) = en(x-1) 1+en (2-1) 0 x>0 otherwise

Step by Step Solution

★★★★★

3.38 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

To show that the sequence of random variables X2 X3 X4 converges in distribution to X 1 we need to d... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Introduction To Probability Statistics Questions!

Q:

In Exercises use LHpitals Rule to evaluate the limit. (In x) lim x1 x 1

Q:

In Exercises, use the properties of logarithms to expand the logarithmic expression. In X 1

Q:

Consider the \(k^{\text {th }}\) central moment functional given by \[T(F)=\int_{-\infty}^{\infty}\left[t-\int_{-\infty}^{\infty} t d F(t)ight]^{k} d F(t)\] where \(F \in \mathcal{F}\), a collection...

Q:

In Example 6.6, find \(\boldsymbol{\Lambda}\) and \(\mathbf{d}^{\prime}(\theta) \boldsymbol{\Lambda} \mathbf{d}(\theta)\). Example 6.6. Let {X} be a sequence of independent and identically...

Q:

A Small Numerical Library Here is header : #ifndef __MATHLIB_H__ #define __MATHLIB_H__ double Sin(double x); double Cos(double x); double Tan(double x); double Exp(double x); double Log(double x);...

Q:

A Small Numerical Library Here is header : #ifndef __MATHLIB_H__ #define __MATHLIB_H__ double Sin(double x); double Cos(double x); double Tan(double x); double Exp(double x); double Log(double x);...

Q:

the amount of the the missing data, and whether we will be able to encompass the selected group of indicator or not. If a lot of data is missing that cannot be imputed meaningfully, we have to...

Q:

deletion O the amount of the missing data, and whether we will be able to encompass the selected group of indicator or not. If a lot of data is missing that cannot be imputed meaningfully, we have to...

Q:

Let x n be a sequence of random variables that converges in distribution to a random variable x . Let Y n be a sequence of random variables with the property that for any finite number c , lim n P (...

Q:

Calculate the price elasticity of demand. a) When the price of a phone call increases from $8 to $12, the volume of calls falls from 25,000 per hour to 15,000. b) New car dealers currently sell...

Q:

Allan borrows $2440 from his uncle. Two years later, he borrows another $1440. If his uncle charges him 8.2% interest compounded annually, how much does Allan owe 9 years after the first loan?

Q:

In order to get out of debt, it is recommended that you do all of the following except: cut up your credit cards. start living on a cash-only basis. try to lower your monthly bills. take out a cash...

Q:

During the early stages of the coronavirus pandemic, did you ever observe conflicting values being expressed by different public figures? Did you see public health officials, government...

Q:

Suppose that, next month, the quality control division will inspect 30 units. Among these, 20 will undergo a speed test and 10 will be tested for current flow. If an engineer is randomly assigned 4...

Q:

With reference to the aluminum-alloy strength data in Example 7, make a stem-and-leaf display. Data From Example 7 EXAMPLE 7 A density histogram has total area I Compressive strength was measured on...

Q:

Find the mean and the standard deviation of the 20 humidity readings on page 31 by using the (a) the raw (ungrouped) data (b) the distribution obtained in that example Humidity Readings 10-19 20-29...

Q:

Help me with this On August 31, 2016, Sarah Thoreau borrowed $8,000 from First State Bank. Thoreau signed a note payable, promising to pay the bank principal plus interest on August 31, 2017. The...

Q:

Nonprofit Organization you are familiar with and state what their accountability would be to the Donor. (ex. Cancer Society must be accountable for what is spent from monies going towards research,...

Q:

If long-term assets are not depreciated, expenses on the income statement: a). will not be affected. b). will be overstated. c). will be understated. d). may be either overstated or understated.