Let X be a binomial random variable with parameters n = 6, p = .4. Then, starting with P{X = 0} = (.6)6 and recursively employing Equation 5.1.4, we obtain

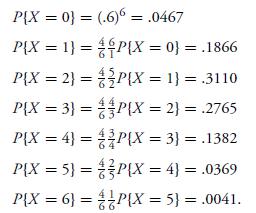
The text disk uses Equation 5.1.4 to compute binomial probabilities. In using it, one enters the binomial parameters n and p and a value i and the program computes the probabilities that a binomial (n, p) random variable is equal to and is less than or equal to i.

P{X=0} = (.6)6 = .0467 P{X = 1}= P(X = 0} = .1866 P{X = 2} = P(X = 1} = .3110 P{X = 3) = P(X = 2) = .2765 P{X=4} = P{X=3} = .1382 P{X = 5} = P(X = 4} = .0369 P{X = 6} = 66 P{X = 5} = .0041.