Let X be a continuous random variable with density function f . We say that X has a symmetric distribution around the point a if we have P(X ≥ a + x) = P(X ≤ a − x)

for any x ∈ ℝ.

(i) Show that the distribution of X is symmetric around a if and only if f (a − x) = f (a + x).

(ii) Establish that each of the following distributions, with densities given below, is symmetric around a point a which should be identified: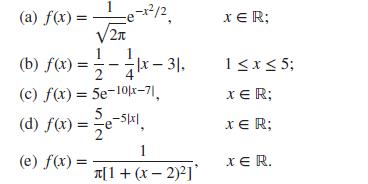

(a) f(x) = e-x/2 XER; 2 (b) f(x)=x -31, (c) f(x)=5e-10|x-71, 5 (d) f(x) = e-skl 2 1x5; XER; x = R; 1 (e) f(x) = XER. [1+(x-2)]